Наука против мифов

Это не я придумал. Есть целое движение - "Учёные против мифов".

Наука начинается с критического отношения к мифам

Карл Поппер, философ и социолог

Замечательно, что мифы не имеют ничего против науки или учёных...
Наоборот — миф или сказка (как производная от мифа) всегда приветствуют исследователя, искателя истины!
Как и в случае с узором (орнаментом), мифы делятся на два вида:
− космогонический, повествующий о создании и устройстве мира;
− обучающий (сказка лож, да в ней намёк...), рассказывающий о пути души: обретении силы, мудрости и возвращении домой.
Яркий пример − Титаномахия и Одиссея.

Но здесь есть тонкость: учёный − не обязательно исследователь.

Учёный

1) О человеке: получивший специальные знания в какой-л. области, выученный, наученный чему-л.
В это время мне предложили место ученого лесничего в Лисинском учебном лесничестве (Шелгунов).

2) О животном: выдрессированный.
Ученая собака.
Ученый медведь.
И там я был, и мед я пил; у моря видел дуб зеленый; под ним сидел, и кот ученый свои мне сказки говорил (Пушкин).

Толковый словарь русского языка

Как член научного сообщества, он больше занят битвой за место, чем поиском истины. В том числе получая очки за борьбу с лженаукой и мифами.

В 40-х годах группа молодых учеников виталистски ориентированного И. Мюллера дала в противовес своему учителю торжественную клятву (подписав ее собственной кровью) объяснять все явления живой природы исключительно в категориях физики и химии.
Эти ученики (среди них были Гельмгольц и Дюбуа-Реймон - будущие корифеи физиологии XIX века) образовали "незримый колледж", вошедший в историю под именем физико-химической школы. Они разрушили виталистские предубеждения и отказались от установки на исключительность психического в общей системе природы.
Вожди этой школы - Гельмгольц, Дюбуа-Реймон, Карл Людвиг, Брюкке и другие - были учителями и вдохновителями тех, кто в последующий период сделал психологию опытной наукой

Ярошевский, История психологии, с. 194

Как вы понимаете, клятва на крови никак не может относиться к поиску истины. Истина сама определит, в каких категориях надо ее объяснять. Ничего, кроме внутринаучной поли-
тики, за этим нет, и похоже, это лишь на тайное общество революционного
или террористического толка…

Титаномахия — война Богов.
Богиня Наука, как всякая женщина, ревнива.
Не я первый обратил внимание, что современная наука по существу говорит ровно то же, что и мифы, но своим особым, "научным" языком.
Например, происхождение Вселенной из первичного яйца.
Или первозвук "Ом", что был первым проявлением не явленного ещё Брахмана, давшим начало воспринимаемой Вселенной, произошедшей от вибрации, вызванной этим звуком...

«Второй закон Пифагора — Архита» и сейчас кажется удивительным. Что же говорить о пифагорейцах, которых он просто привел в восторг. Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение Вселенной.
[...]
Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду. В конце концов эта идея приняла «космические
масштабы» и переросла в идею «всеобщей гармонии». Пифагорейцы утвердились в
том, что вся Вселенная устроена на основе музыкальных, т. е. простых числовых, соотношений, что движущиеся планеты издают «музыку небесных сфер», а обычная
музыка является лишь «отзвуком» царящей всюду «всеобщей гармонии». […] Но безудержный полет фантазии увлекал античных мыслителей все дальше, в заоблачные дали, в поиски всемирной «космической музыки». И хотя поиски эти оказались бесплодными, а античная космология с современной точки зрения кажется слишком наивной, не нужно спешить смеяться над нашими предшественниками…"

А.В. Волошинов, "Математика и искусство"

Не станем спешить.

Передний край современной науки - квантовая теория - как раз описывает мир как «волновую функцию». И раскладывает на составляющие части - ряды Фурье!
А вы знаете, что такое ряды Фурье?

Статья, даже научно-популярная про преобразование и ряды Фурье бесполезна. Это самые мощнейшие аналитические инструменты, которые знает человечество. Место, где инженерная мысль граничит с магией. По этому вопросу пишут монографии, и единичные статьи почти ничего не охватят.

Константин Бурлаченко, Frequently Asked Questions about Fourier Transform

Страшно? Отож.
Константин Бурлаченко - учёный! Он обязан изъясняться сложно - на этом держится очарование Науки.
Но если ты не боец научного сообщества, можно о том же рассказать просто.
Фурье предположил, что любой с виду неупорядоченный шум состоит из суммы нескольких простых частот. Вот так:

Сложность состоит в нахождении этих исходных частот. И делается это весьма остроумно - закольцовыванием и намоткой некоего участка волнового изображения на ось:

Другими словами, безконечный ряд представляется в виде кольца.

Насколько это допустимо с точки зрения классической математики?
Да вполне!
Вот формула Тейлора повествует о разложение функции в бесконечную сумму степенных функций:

Здесь Алексей Савватеев объясняет почему знакочередующийся ряд в итоге равен π/4.

Или взять знаменитое тождество Эйлера, где ряд обратных квадратов оказывается равным π²/6.

Надо ли говорить, что бесконечность всегда связывалась с кругом Жизни или колесом Сансары?
Другими словами, бесконечность — это не прямая, а круг или вращение.

Многие физические формулы так же имеют двойное представление.

Одной формулой описываются два вида движения: возвратно-поступательное и вращательное.

Связь и взаимозаменяемость прямолинейного и кругового движения очевидна.
Да и как ей не быть, если синус и косинус являются катетами треугольника, гипотенуза которого есть радиус единичной окружности?
Дело в том, что первые же шаги Творения производят основания квадратов с площадями 1, 2, 3, 5, что так же позволяет работать с "иррациональными" числами без потери точности. А так же поделить окружность на 2, 3 и 5 равных частей (см. построение равностороннего треугольника и пятиугольника).

Но ещё более примечательна связь физических и геометрических формул. Разве не похожи формулы кинетической энергии и площади круга?
А если π заменить на τ ?
Работать с τ гораздо удобнее просто потому, что круг - это один оборот. Как проще объяснить ребёнку в школе, что такое четверть оборота: π/2 или τ/4 ?

Непременно ознакомьтесь с "Манифестом Тау" Майкла Хартли, там таких примеров множество.

А что с теорией вероятности?
Случайность, вероятность, жребий, удача, судьба...
Мифологически это снова круг, колесо Фортуны!
А что говорит Наука?
Вы будете смеяться, но вся теория вероятности и распределения событий полностью завязано на π и e.

Количество попыток, бросков кубика или выстрелов всегда целое. Но с ростом n форма биномиальной фигуры распределения становится похожа на плавную кривую Гаусса. Об этом повествует Теорема Муавра — Лапласа:

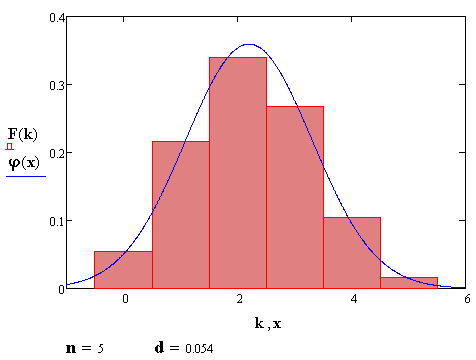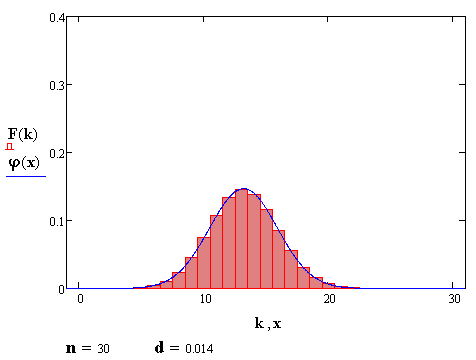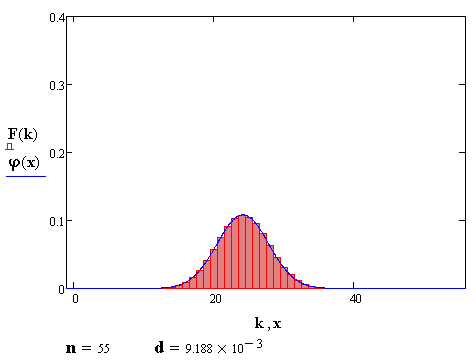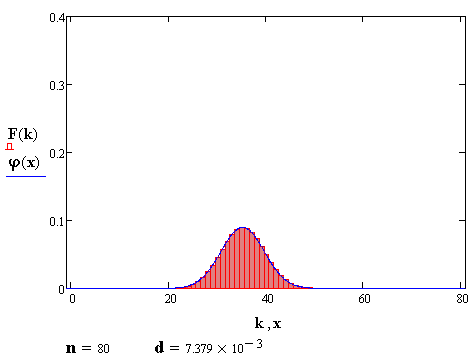
А следующий ролик начинается с анекдота о социологе, который пытается объяснить приятелю, что законы статистики и социологии определяются через отношение длины окружности к её диаметру.

Количество членов общества не может быть дробным.

Дидье Дезор, исследователь лаборатории биологического поведения университета Нанси (Франция), провел исследование поведения крыс, которое показало результаты, интересные для психологов.
С целью изучения плавательных способностей крыс он поместил в одну клетку шесть зверьков. Единственный выход из клетки вел в бассейн, который необходимо было переплыть, чтобы добраться до кормушки с пищей.
В ходе эксперимента выяснилось, что крысы не плыли вместе на поиски пищи. Все происходило так, как будто они распределили между собой социальные роли: были два эксплуататора, которые вообще никогда не плавали, два эксплуатируемых пловца, один независимый пловец и один не плавающий козел отпущения.

Социальная иерархия: эксперимент с крысами

Такое впечатление, что места в обществе, как за княжеским столом, предопределены.
Мы, как участники, лишь занимаем их на какое-то время в соответствии со своими достоинствами.
Чем больше участников — тем подробнее происходит деление.
Если участников очень много — то происходит фрактальное повторение.

Удивительно наблюдать, как поведение и численность вида подчиняется строгим математическим законам.
Самый простой случай - рождение самцов и самок (мальчиков и девочек, если говорить о людях) примерно в равных количествах.
В ролике Veritasium "Уравнение, которое меняет взгляд на мир" показано, как простое уравнение x_n+1=rx_n(1-x_n) точно описывает пределы и скачки популяции различных животных (например, кроликов).

А можно сказать иначе — это закон, который определяет эти пределы и изменения.

Как происходит назначение переменных? Где та база данных, в которой ведётся учёт?
По каким признакам определяются (накладываются) пределы группы?

При R меньше 1 любая популяция вымирает, стационарное значение 0.
Стоит коэффициенту R пересечь единицу, популяция растёт, пока не достигнет равновесного значения. И чем выше R, тем оно будет больше.
Какое-то время всё стабильно, а потом начинается кое-что любопытное.
При R больше 3 график делится на 2.
Численность популяции будет колебаться между двумя значениями.
Значения будут расходится всё дальше, а замем снова разделяться.

Vert Dider, "Уравнение, которое меняет взгляд на мир"

Однако, дальше ещё удивительнее.

Возможно, вы заметили, что эта бифуркационная диаграмма напоминает фрактал. Её общий вид очень похож на отдельные элементы, когда их приближаешь. Можно безконечно увеличивать изображение и рисунок будет повторяться.
Да, это фрактал.
Один из наиболее известных примеров фрактала - множество Мандельброта.
Бифуркационная диаграмма - это часть множества Мандельброта.
Такой вот поворот...

Vert Dider, "Уравнение, которое меняет взгляд на мир"

А есть ли вообще разница между законами физики, социологии и геометрии? И насколько оправдано говорить о многих законах? Даже если закона всего два и они противоречат друг другу, то мир не состоится. А если противоречия нет - значит всё наблюдаемое нами множество законов есть следствие единого, исходного.

В.И. Арнольд говорит, что математика — это часть физики.
А я дополняю: физика — часть геометрии!

И.Ф. Шарыгин

Ну это давняя история.
Пифагор полагал геометрию основой всех наук.
Потом математики показали, что уравнения имеют отрицательные решения, да ещё придумали мнимые числа и заявили, что "освободились" от геометрии.
Геометры тут же нарисовали комплексную плоскость и показали красивейшие решения на ней (формула Абрахама де Муавра).

Ритуал посвящения в члены пифагорейского братства был окружен множеством таинств, разглашение которых сурово каралось. Но и попав в орден после строгого отбора и испытательного периода, новички могли только из-за занавеса слушать голос Учителя, видеть же его самого разрешалось только после нескольких лет аскетической жизни. «Стремление уйти от мира, замкнутая монашеская жизнь, вегетарианство и общность имущества встречались у многих сект. Но что отличало пифагорейцев от всех других — это способ, при помощи которого они считали возможным достигнуть очищения души и соединения с божеством; это делалось именно при помощи математики. Математика была одной из составных частей их религии».

Эта меткая характеристика пифагорейского братства принадлежит известному голландскому математику и историку науки Б. Л. ван дер Вардену.
Итак, именно в математике, в познании количественных отношений, видели пифагорейцы ключ к разгадке мировой гармонии, постижение которой и составляло смысл их жизни. Но почему постижение всеобщей гармонии ставилось высшей жизненной целью? Дело в том, что пифагорейцы верили в бессмертие души и переселение души человека в животных. Поэтому они полагали, что посвящение в тайны всеобщей гармонии, т. е. стремление к истине, приближает душу человека к божеству, создавшему эту гармонию, вследствие чего душа сможет освободиться от дальнейших перевоплощений .

А.В. Волошинов, «Математика и искусство»

Законы математики и геометрии вечны и неизменны. Это те самые законы Рита, которым подчиняются даже Боги.
Классические построения с помощью циркуля и линейки по сути повторяют первые шаги творения и раскрывают законы, которые устраивают прекрасный порядок и правят всем мирозданием.
Кто живёт вечным - тот живёт вечно...
Ну а когда дело дошло до дифференциалов и интегралов, тут уже всем стало ясно, что лучшего представления, чем графики кривых и площадей под ними уже не придумать.

Суть ответа кроется в замечании, которое физик Ричард Фейнман сделал во время обсуждения Манхэттенского проекта с писателем Германом Воуком. Воук собирал материал для крупного романа о Второй мировой войне, который планировал написать, и отправился
в Калтех[2], чтобы побеседовать с физиками, работавшими над созданием бомбы, а Фейнман был одним из них. Когда они прощались после интервью, Фейнман спросил Воука, знает ли тот матанализ. Воук признался, что нет. «Вам следовало бы ему поучиться, – сказал Фейнман. – Это язык, на котором говорит Бог»[3].
Действительно, Вселенная – глубоко математическая сущность[4], хотя причин этого явления никто не понимает. Возможно, так устроил Бог. А может, это единственный способ нашего в ней существования, ибо нематематические вселенные не могут создать жизнь, достаточно
разумную для того, чтобы задать такой вопрос. В любом случае то, что наша Вселенная подчиняется законам природы, которые всегда выражены на языке анализа в виде предложений, называемых дифференциальными уравнениями, – весьма таинственный и изумительный факт. Такие уравнения описывают разницу между чем-то прямо сейчас и той же величиной мгновение спустя или между чем-то прямо здесь и бесконечно близко. Детали отличаются в зависимости от конкретной области природы, но структура законов всегда одна и та же.
Иначе говоря, все выглядит так, словно у Вселенной существует какой-то код, некая операционная система, которая оживляет все в конкретный момент в конкретном месте. Анализ подключается к этому порядку и выражает его.
Исаак Ньютон первым увидел эту тайну Вселенной. Он обнаружил, что орбиты планет, ритм приливов и отливов и траектории пушечных ядер можно описать, объяснить и предсказать с помощью небольшого набора дифференциальных уравнений. Сегодня мы называем их законами движения и гравитации Ньютона. Мы обнаружили, что эта закономерность сохраняется всякий раз, когда мы открываем какую-то новую часть Вселенной. От старых стихий – земли, воздуха, огня и воды, до новейших электронов, кварков, черных
дыр и суперструн – все во Вселенной подчиняется правилам дифференциальных уравнений. Бьюсь об заклад, что именно это имел в виду Фейнман, когда говорил, что на этом языке разговаривает Бог.
Если что-то и заслуживает называться тайной Вселенной, то это дифференциальное исчисление.

Стивен Строгац, "Бесконечная сила"

Точность

Геоглиф Estrella показывает самое начало построения многоугольника, стремящегося стать окружностью удваивая точность с каждым новым шагом. По сути, основу дифференциального исчисления.

Как измерить длину кривой или объём бочки?
Представить окружность или дугу в виде многоугольника или ломаного отрезка!
Так вычисления становятся возможными, да ещё с высочайшей точностью!
При этом физики и математики стыдливо говорят, мол это лишь мы так воображаем, а на самом деле пространство и материя непрерывны.

Так начинался анализ. Он рос из любопытства геометров и разочарования в округлости. Круги, сферы и прочие изогнутые формы были Гималаями той эпохи. И не потому, что они ставили важные практические задачи, по крайней мере поначалу. Дело было в жажде
приключений, характерной для человеческого духа. Подобно покорителям Эвереста, геометры хотели разобраться с кривыми просто потому что они есть.
Прорыв произошел благодаря идее, что кривые на самом деле состоят из прямых частей. Хотя это неправда, но можно сделать вид, что это так. Загвоздка была в том, что тогда эти части должны быть бесконечно малы и бесконечно многочисленны. Благодаря такой фантастической концепции родилось интегральное исчисление.

Стивен Строгац, "Бесконечная сила"

Суть дифференцирования - дробление на "бесконечно малые" части.
Но насколько это отражает действительный мир?

Хотя квантовая механика во многих отношениях оперирует радикально новыми концепциями, она сохраняет традиционное предположение о непрерывности пространства и времени. Максвелл делал аналогичное предположение в своей теории электромагнитных волн, Ньютон – в теории тяготения, Эйнштейн – в теории относительности. Весь анализ, а следовательно, и вся теоретическая физика опираются на предположение о непрерывности пространства и времени. До сих пор оно приводило к ошеломляющим успехам.

Однако есть основания полагать, что в масштабах гораздо ниже атомных пространство и время теряют непрерывный характер. Мы не знаем, что действительно происходит на этом уровне, но можем строить догадки. Может оказаться, что пространство и время так же
«пикселизированы», как в парадоксе Зенона «Стрела», хотя более вероятно, что из-за квантовой неопределенности они вырождаются в беспорядочный хаос. В таких малых масштабах пространство и время могут случайным образом бурлить и волноваться. Они могут меняться, как пузырящаяся пена.

Хотя в вопросе, как представлять пространство и время в этих масштабах, пока согласия нет, есть консенсус в отношении самих этих масштабов. Они определяются тремя фундаментальными константами природы, одна из которых – гравитационная постоянная G Она измеряет силу тяготения во Вселенной. Сначала эта константа появилась в ньютоновском законе всемирного тяготения, а затем в общей теории относительности Эйнштейна. Она будет и в любой теории, которая их заменит. Вторая постоянная ħ (читается «h с чертой») отражает силу квантовых эффектов[40]. Она появляется, например, в принципе неопределенности Гейзенберга и в волновом уравнении Шрёдингера, использующемся в квантовой механике. Третья константа – это скорость света c. Это максимальная скорость во Вселенной. Никакой сигнал не может распространяться со скоростью, превышающей c. Эта скорость должна обязательно входить в любую теорию пространства и времени, поскольку связывает их: расстояние равно произведению скорости и времени.

В 1899 году отец квантовой теории немецкий физик Макс Планк понял, что есть единственный способ объединить эти фундаментальные константы для получения единицы длины. Он пришел к выводу, что такая единица – естественная «мера длины» во Вселенной. В его честь она именуется планковской длиной[41] и определяется следующим соотношением: Если подставить измеренные значения ħ, G и c, то планковская длина оказывается равной около 10^–35 метра – ошеломительно малое расстояние, которое примерно в сто миллионов триллионов раз меньше диаметра протона. Соответствующее планковское время – это время, за которое свет проходит такое расстояние, и оно приблизительно равно 10^–43 секунды. При меньших величинах пространство и время теряют смысл.

Эти числа ограничивают наши возможности деления пространства и времени. Чтобы ощутить уровень точности, о котором мы говорим, посмотрим, сколько цифр нам понадобится для проведения одного из самых экстремальных сравнений. Возьмем самое большое возможное расстояние – оцениваемый диаметр Вселенной, и разделим его на самое маленькое возможное расстояние – планковскую длину. Это невообразимо огромное отношение расстояний выражается числом, состоящим всего лишь из шестидесяти цифр. Хочу подчеркнуть – всего шестидесяти. И это самое большое число, которое понадобится, чтобы выразить одно расстояние через другое. Использование большего количества – скажем, сотни цифр, не говоря уже о еще больших числах – было бы колоссальным излишеством, не требующимся для описания каких-либо реальных расстояний в материальном мире.

Стивен Строгац, "Бесконечная сила"

Представить бесконечное деление легко: вот мы взяли некий предмет и поделили его пополам.
Потом ещё пополам. Потом ещё... и ещё... и ещё...
Гораздо трудней представить, что однажды мы дойдём до части, которую поделить нельзя.
Как так-то?!
Тем действительный, явный мир отличается от мнимого, навного.
Математические ряды бесконечны — здесь нет препятствий к делению или увеличению. Но, предположим, мы пресытились созерцанием бесконечности и хотим наконец, что то сделать.
Для этого нам нужно выделить некий член ряда (отрезок) и принять его за Единицу.
И что бы мы не делали далее, всё будет соотносится именно с ней!

Миф прямо говорит о начальной единице. Отсюда издевательские апории Зенона об Ахиллесе и черепахе или стреле, застывшей в полёте.
Ведь если нет меры, то как отличить большое от малого?
«Наука начинается там, где начинаются измерения» — утверждал Дмитрий Иванович Менделеев.
Что так же подтверждает необходимость Меры, неделимой Единицы, как пространства, так и времени, которые имеют один источник.
При этом наука строго вторична по отношению к исследуемому предмету. В широком смысле - к Творению.
Другими словами: то, что исследователь называет мерой, для Творца является инструментом, орудием творения!

Сплошные кривые невозможно измерить. А значит и построить!
Отсюда следует простой вывод - мир дискретен. Материя состоит из мельчайших неделимых частиц. Пространство размечено на крохотные частицы (клеточки или кубики - как посмотреть).
Любая окружность являет себя многоугольником с огромным, но не беcконечным количеством сторон!

Материальный отрезок (или если смотреть шире - пространство) невозможно точно поделить в золотом отношении. Но чем больше будет частиц, составляющих его, тем точнее будет будет приближение — ряд Фибоначчи.

Пифагорейцы считали Единицу неделимой именно потому, что говорили о таинстве Творения, а не "абстрактной" математике. А для счёта использовали камушки, называемые calculus (отсюда наш "калькулятор"). Камушками прекрасно можно показать количество и целочисленные отношения. При этом они свободны от ограничений какой-либо системы счисления, а значит от ошибок, как в случае с современным калькулятором.
Простой пример: разделите на компьютере или калькуляторе 1 на 3, а потом снова умножьте на 3. Получим 0,999(9)...

Без системы счисления можно вполне обойтись в начале...
Но если речь идёт о размерности в сотнях или тысячах камешков?

Любая система счёта подразумевает деление окружности и бесконечное повторение.

Мы привыкли, что длина окружности равна 3,14…∞ её диаметра. Но такое представление полностью привязано к «культурному контексту»: нужно знать числа и пользоваться именно десятичным счислением! А десятичный счёт далеко не всегда хорош.
Большие числа мы считаем десятками и сотнями неосознанно деля окружности на 10 частей - стремимся округлить.
Но в действительности деление круга на 12 частей востребовано чаще - как в случае с музыкальным звукорядом, состоящим, напомню, из 12 ступеней или делением года на месяцы. Или дня на часы.
Число 12 удобно тем, что делится на 3 и 4 являясь частью шестидесятеричной системы счисления, которой мы пользуемся с незапамятных времён по сей день.
Десятичная система, так же являясь частью шестидесятеричной, делится на 2 и 5.
Пользоваться шестидесятеричной системой не очень то удобно - больно громоздкая.
Поэтому, вместо шестидесятеричной системы использовали по обстоятельствам дополняющие друг друга десяти- или двенадцатеричную.

Но как быть с иррациональным числами?

По преданию, Пифагорейцы были потрясены открытием иррациональных чисел, вроде диагонали квадрата, которые невозможно выразить целочисленными отношениями.
Я позволю себе в этом усомниться.

Открытие несоизмеримости (для диагонали квадрата со стороной 1 не было соответствующего числа) опрокидывало всю философскую систему пифагорейцев, которые были убеждены, что «элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом».
Это открытие долго держалось в тайне, а ученик Пифагора Гиппас из Метапонта за то, что он открыл недостойным участия в учениях природу пропорции и несоизмеримости, был изгнан из школы Пифагора.
Позднее, когда Гиппас погиб во время кораблекрушения, его противники видели в
этом наказание богов за разглашение тайны.

Волошинов А.В., «Математика и Искусство»

Ещё раз: "... за то, что он открыл недостойным ...".
Они знали. Но хранили в тайне.

Как же производить безупречные вычисления, если "иррациональными числами" буквально пронизана вся математика и геометрия?
Ответ настолько же прост, насколько неочевиден: использовать несколько мер!
Оказывается, во всём мире раньше так и было.

Современная математика разделяет числа на несколько видов:

Древние использовали двенадцать основных мер, разделяя их по признакам кратности 3, 4, 5 и n√2:

Но разве иррациональные числа ограничиваются n√2?
Я вижу здесь удивительную подсказку, намёк...

Корни из целых чисел геометрически являются основаниями квадратов с целочисленными площадями: площадь окружности, построенной на любом отрезке "циркулем и линейкой" будет целочисленной относительно исходной единичной.

Другими словами, что бы избежать иррациональных вычислений над отрезками с размерностью n√m (где n,m - целые числа) нужно уйти в площади.

Особо здесь выделяется ряд "золотого сечения".
В геометрическом представлении это отрезок, рассечённый на две неравные части, где меньшая относится к большей, как большая ко всему отрезку. А сам отрезок является меньшей или большей частью другого отрезка.
Части в свою очередь так же поделены на подобные же кусочки.
К слову сказать, классически это делается через построение звёздчатого пятиугольника со стороной √5-1:

Как работать с такими отрезками без погрешности?

Дело в том, что золотосеченный ряд имеет замечательное свойство:
поскольку 1+Ф=Ф², то Ф^n-2+Ф^n-1=Фⁿ
Что снова позволяет работать с целыми числами (Единицей и степенями Ф) не теряя точности!

То же касается работы с основанием натурального логарифма — числом e.

Все прочие иррациональны числа связаны так или иначе связаны с кривыми или π.
Как я уже выяснил, дуги и окружности в действительности являются ломаными линиями или многоугольниками, что опять же возвращает нас к квадратам и пифагоровым тройкам.
Это приводит к любопытному предположению: возможно ли, что количество таких мер ограничено и в расчётах действительно можно обойтись их целочисленными отношениями не прибегая к бесконечным десятичным (или любым другим) иррациональным дробям?

Полагаю именно так и рассуждали древние.

Но так же мы знаем, что они не использовали (не умели/не хотели) числа отрицательные!
Как так? У нас тут целый прорыв в науке благодаря изобретению мнимой единицы, а им там всё равно..?

Для ответа на этот вопрос я снова обращусь к мифологии.

Счёт

Математика — не наука, а язык для точного описания соразмерностей.
Числа — слова этого языка, которые указывают, значат на нечто сущностное: отрезки, кривые, площади, объёмы...
Либо не имеют смысла.

Следовательно числа имеют начало — это точка.

Потом — луч.
На луче определяется мера — шаг (аршин). Единица.
Следующий единственно возможный шаг —очерчивается круг.

Так появляются ещё две меры - длина границы и площадь окружности.
Они разные потому, что невыразимы друг через друга.
Можно сказать "длина окружности с радиусом 1".
Можно сказать " площадь круга с радиусом 1".
Но площадь невозможно выразить радиусом.
Площадь фигуры выразима только площадью других подобных фигур. Площадь круга лишь приблизительно можно выразить площадью квадрата (или квадратов).
Но так же длина окружности лишь приблизительно выразима через радиус.
А для точного выражения используется другая мера — π или τ.

Луч задал направление. Поскольку мы работаем с плоскостью, назовём его Север.
Ещё луч определил на окружности точку, что позволяет делать следующие шаги безошибочно.
Круг (как впрочем любая прямая или кривая) является безмерной бесконечностью, поскольку его можно делить на бесконечное количество частей. А определить точки можно лишь пересечением с другой прямой, окружностью, кривой, эллипсом или другой фигурой, построенной по закону.

Очевидный следующий шаг - направить луч в противоположную сторону, тем самым разделив окружность на две части - раздвоить.
Был Один — Един. Стала пара противоположностей.

Появляется пространство вероятностей с биноминальным распределением: Да — Нет, Орёл — Решка и т.п.
На первом шаге его не было - возможность совпадала с вероятностью.

Кроме того у нас появилась новая мера - двойной шаг, он же малая сажень.
Теперь можно строить окружности радиусами 2ⁿ сочетая их между собой.
Прострой приём удвоения являет целый путь!

При построение второй окружности возникает новая мера — отрезок √3, он же радиус окружности площадью 3τ/2.

Исходная окружность делится на три равные части, появляются три направления.

Выражение "квадратура круга" имеет исходное значение "площадь круга". А квадрат на Руси называли "четверогранник".
С детства нас приучают мерять площадь квадратами. Но нарисовать квадрат не так уж просто - для этого нужна несущая разметка из окружностей.
Измерять площадь окружностями часто удобнее и точнее.
Окружность - первична.

Следующая по порядку появления фигура, как мы видим - треугольник.
Любопытно, как производить запись, что бы с первого взгляда было понятно идёт ли речь о площади, объёме или длине без обозначения меры?
Выше я написал площадь круга в аршинах.
Обычно принято так: 3τ/2 А².
Но если в работе используется несколько мер и переменных (неизвестных), то букв становится много и их сложно различать. Можно подумать, что там написано "три тау разделить на два квадратных аршина".

При этом важно понимать, с какой мерой ты сейчас работаешь.
По школьным правилам математики 1² = 1.
Это потому, что площади и объёмы всегда основаны на погонных мерах.
Т.е. построения большей мерности происходят из построений меньшей. Если на плоскости можно изобразить отрезки ограниченного числа мер, то количество кубов, шаров и прочих фигур так же будет ограниченно!
К примеру, задача удвоения куба сводится к вычислению длины ребра: кубического корня из 2.
Производя запись "1² = 1" мы как-бы говорим: "длина стороны квадрата площадью 1 равна 1". Но меры то разные и друг через друга невыразимые!

Троичный путь

Удивительно и прекрасно наблюдать, что исходная окружность несёт на себе шесть таких же и делится лучами на 12 частей.

12 содержит в себе одновременно троичный и четверичный путь — каждый со своими особенностями.

Треугольник 1
Периметр - 5.1962
Площадь - 1.299

Треугольник 2
Периметр - 10.3923
Площадь - 5.1962

Треугольник 3
Периметр - 20.7846
Площадь - 20.7846

Здесь можно говорить об особой мере, присущей троичному пути. Назову его Трикветр ☘.
☘ ≈ 1.299 А;

Почему приблизительно?

Длина стороны правильного треугольника, как и его площадь содержит в себе иррациональное число - √3. Это как тамга, обозначающая принадлежность к роду или племени. Ею отмечены формулы всех многоугольников, относящихся к троичному пути.

В нашем случае периметры и площади иррациональны по отношению к аршину.
А если хочется быть точным, то так и надо говорить - площадь треугольника, вписанного в окружность с радиусом 1 аршин. Или просто 1 трикветр;)

Тогда:

Треугольник 1
Периметр - 4☘
Площадь - 1☘

Треугольник 2
Периметр - 8☘
Площадь - 4☘

Треугольник 3
Периметр - 16☘
Площадь - 16☘

Радиус окружности удваивается на каждом шаге: 1,2,4 аршина соответственно.

Здесь тоже можно вывести общую формулу отношения радиуса к периметру:
1A ∼ 4☘
Площадь можно выразить как степень четвёрки: 4⁰ , 4¹ , 4² и т.д.
Уж здесь я получаю ответ, как древние обходились без отрицательных чисел: счёт всегда положительный, но в разных направлениях от середины — по лучам.

Не могу утверждать, но предположу, что важность имеют лепестки, возникающие при пересечении окружностей — именно они образуют меры.
В случае троичного пути таких способов соединения немного: два треугольника или шестиугольник.
Пропорции очень просты: стороны треугольников делятся на три равные части, которые так же являются и сторонами вписанного шестиугольника.
Но не могу не отметить, что периметр шестиугольника равен 6 аршинам, а площадь - 2 трикветрам ☘ 😉

Моя задача здесь — наметить пути, а не пройти их. Поэтому я не стану рассматривать другие многоугольники с количеством сторон, кратных трём. Там тоже есть занимательные закономерности, но сложность возрастает и такой изящной простоты как в начале уже не будет.

Четверичный путь

Громовник позволил построить боковые лепестки и лучи Восток-Запад, на которых можно построить боковые окружности и получить новые меры:

Четверичный путь достаточно подробно исследован, поскольку является основой саженного строя, а так же похож на привычные всем декартовы координаты. За той лишь разницей, что здесь не две оси, а четыре луча.

Основное отличие от троичного пути в том, что удвоение радиуса происходит не на каждом шаге, а через один, перемежаясь Царской саженью, равной Малой×√2 .

На каждом шаге удваивается площадь квадрата.
Периметр и площадь меряются малыми, царскими или городовыми саженями.

Концы лепестков можно соединить следующими способами:

• два повёрнутых квадрата
• восьмиугольник
• звёздчатый восьмиугольник

Каждый случай порождает свои пропорции, но все они так или иначе связаны с √2.

У нас образовались три меры:
X = 1,53073373
Y = 1,1715728753
Z = 0,8284271247

Только вот незадача: Z получилась меньше единицы, что недопустимо.
Это значит, что такое построение возможно лишь на окружностях радиусом √3 и более.
Однако, пропорции от этого не изменятся — приведу их:

X/√2 = Z+1
Y/√2 = Z
X²=Y×2
Z=2×√2 - 2

Напомню, что √2 — это Царская сажень.
А значит X,Y,Z всего лишь производные простых арифметических действия, проводимых с Малой и Царской саженями. Т.е. целочисленные вычисления.

Те же качества наследует и звёздчатый восьмиугольник.
Для наглядности приемственности я изобразил его на розетке из окружностей радиусом 2 аршина:

Здесь:
a=0,6340506711
b=0,896683058
c=1,53073373
d=3,061467459
e=3,69551813
f=5,22625186

b/a=√2
c=X=√2Y
d=2C
e/c=1+√2
f/e=√2
Это всё хорошо, но назрел вопрос о пятеричном пути.
Благодаря "громовому колесу" мы легко поделили окружность на 6 и 8 частей.
Продлить эти ряды не составит труда. Но ни один их член не будет кратен пяти.

Далее следуют удивительные и не всегда очевидные шаги.

Пятеричный путь

"Школьный" способ построения пятиугольника выглядит так:

В кавычках, поскольку он вовсе не детский, а был взят из "Альмагеста" Клавдия Птоломея.

«Альмаге́ст» (лат. Almagest, от араб. الكتاب المجسطي‎, аль-Китаб аль-Маджисти — «Великое построение», также «Великое математическое построение по астрономии в 13 книгах») — классический труд Клавдия Птолемея, появившийся около 140 года и включающий полный комплекс астрономических знаний Греции и Ближнего Востока того времени. «Альмагест» на протяжении тринадцати столетий оставался основой астрономических исследований.

W:Альмагест

Очевидно, Птоломей не сам придумал его, а взял из более древних источников.

Обычно никто не объясняет, почему надо делать именно так.
«Сначала ставим циркуль сюда, потом сюда, хоп-хоп — готово!".

1. Ножка на перекрестии осей, чертим единичную (так и говорят!) окружность. Откуда взялись оси — упускается. А ведь для их тоже нужно как-то получить...

2. Чертим полуокружность (а по сути лепесток розетки четверичного пути) что бы разделить радиус пополам.
Но древние не делили Единицу!
Шаг, аршин — наименьшая начальная мера.
Это правило относится не только к Пифагорейской школе, но ко всем мировым культурам!

3. Откладываем дугу BA. Проведя некоторые следственные мероприятия выясняем, что это √5 и мы движемся к "золотому сечению". Позвольте! Но √5 — это диагональ сдвоенного квадрата! Другими словами, радиус мы принимаем за 2, стоим прямоугольник со сторонами 2:1 после чего откладываем его диагональ на горизонтальную ось. Так мы получили отрезок BA, равный стороне пятиугольника. Ух ты!

4. Проводим дугу через А откладывая сразу две стороны пятиугольника и далее оставшиеся.

Как до этого вообще можно было додумать? Какое рассуждение сюда привело?

Попробую повторить построение самостоятельно в меру своего разумения.

За основу берётся розетка четверичного пути — Коловрат.
Треугольник COB имеет отношения сторон 1 : 2 : √5.
Откладываем гипотенузу на горизонтальную ось, получаем треугольник AOB с отношениями сторон (√5-1) : 2 : X, где X - искомая сторона пятиугольника.
Чему же она равна?

По определению (√5-1):2 есть отношение золотого сечения.
У золотого ряда есть замечательное свойство:
φ²=1-φ
Но что бы им воспользоваться наш большой катет должен быть равен 1. А он равен двум!
Что делать?
Можно просто условиться: примем большой катет за 1. А что бы не запутаться, дадим этой мере отдельное имя: Малая сажень!

— А если радиус 3 аршина?
— Казённая сажень!

— А если 4 аршина?
— Снова малая сажень, но в масштабе ×2. Или на языке музыки — во второй октаве.

— А если 5 аршин?
— Народна! Ведь она относится к Малой как 5 к 4 !

Все сажени кратны 3,4,5 и √2. Их всего 12, потом всё повторяется в удвоенном масштабе (см. "Строй").
Самое мелкое дробление у Большой сажени. Она соотносится с Малой как 15 : 8, а значит появляется лишь в третьей октаве (или масштаб ×3).
Удивительный математический приём!

Однако, вернёмся к нашему золотому треугольнику.

(X/2)²=1²+φ² #Сумма квадратов катетов равна квадрату гипотенузы

X/2=√(1²+φ²)=√(2-φ) #Размер стороны пятиугольника в Малых саженях

Математически безукоризненно, но как можно додумать до этого построения?!

— Я тут хочу разделить окружность на пять частей. Не соображу, какого размера там должна быть сторона пятиугольника...
— Может √(2-φ) ?
— Хм, надо попробовать... Да, точняк! Спсб!

Типичная беседа пифагорейцев

Но кое-что я понял.
Невозможно построить пятиугольник на единичной окружность. Нужна окружность с радиусом 2 аршина, которая естественно образуется из "Громовника".

Получается последовательное рассуждение: 6 и 8 порождают 10.
Что так же согласуется с мифологией: тройка и четвёрка порождают пятёрку!

СОРОК СЕДЬМАЯ ТЕОРЕМА ЕВКЛИДА

Истинным ключом к философской математике является сорок седьмая теорема Пифагора, ошибочно приписываемая Евклиду. Сорок седьмая теорема утверждает следующее: в прямоугольном треугольнике квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах. Относительно этой проблемы Плутарх писал: «Универсальная природа, в своем самом полном и совершенном виде, состоит, согласно современному учению, из трех вещей: Разума, Материи и взаимного их результата, называемого на греческом языке Космосом, словом, которое означает как красоту и порядок, так и сам мир. Первое из них есть то же самое, что Платон имел обыкновение называть Идеей, или Отцом; второму из них было дано имя Матери, Кормилицы или Места Порождения. Третьему — имя Отпрыска, или Продукта. Таким образом, как и в случае египтян, есть основательные причины для того, чтобы считать, что пифагорейцы имели обыкновение уподоблять эту универсальную Природу тому, что они называли наиболее прекрасным и совершенным треугольником. То же самое имеет в виду Платон в своем „Государстве“, когда вводит условия брачного союза. В этом треугольнике с прямым углом, с перпендикулярной стороной, равной трем, основанием, равным четырем, и гипотенузой, равной пяти, перпендикулярная сторона представляет мужскую природу, основание — женскую и гипотенуза — отпрыск двух первых. И потому первая сторона должна представлять Осириса, или первую причину, вторая — Исиду, или восприимчивую силу, и последняя — Оруса (Хоруса), общий результат первых двух. Потому что три есть первое число, которое составлено из четного числа и нечетного числа, а число четыре есть квадрат, сторона которого равна четному числу два. А число пять, будучи порождено из предшествующих чисел два и три, имеет равное отношение к предшествующим двум как общим родителям» (см. «Исида и Осирис»).

По этому поводу Кирхер пишет: «Из самых простых линий и фигур возникает целая тайна природы телесного мира. Точно так же, как троица круга (центр, радиус и окружность) показывает Божественную Троицу, так и творческая работа Божественной Троицы проявляется в троичности равностороннего треугольника. Круг не порождает ничего сам по себе, будучи уже завершенным, состоящим из бесконечного числа сторон. Это самый большой из всех многоугольников и поэтому является единой троицей. Но треугольник есть начало всех порождений, будучи прародителем всех других многоугольников или тел. Следующим идет равнобедренный треугольник, символ земли и небесного свода. Далее идет прямоугольный треугольник, который содержит всю тайну порождения природы. Этот треугольник, как уже было сказано, есть треугольник с неравными сторонами, с одним прямым углом и двумя острыми углами. Прямой угол означает постоянство и неизменность действия закона природы; больший острый угол — усиливающееся движение, а меньший — уменьшающееся. Стороны имеют длину соответственно 3, 4 и 5. Заметим, что 3 + 4 + 5 = 12; природа этого числа представлена додекаэдром. Отсюда, точно так же, как числа в неявном виде содержатся в числах, линии — в линиях и фигуры — в фигурах, так и все содержится во всем. И это положение выражено здесь оккультным образом» (А. Кирхер. «Эдип Египетский»), Кирхер далее добавляет, что из прямоугольного треугольника происходят все земные тела и вся вселенная.

Мэнли Холл, "Энциклопедическое изложение символистской философии"

Ещё я понял, что у пятеричного ряда тоже есть своя тамга - √5. Закон работает!

Мерами пятеричного пути будут члены золотого ряда:
Ф = (√5+1):2;
φ = (√5-1):2;

Но я хочу знать рассуждение, которое привело к такому способу построения пятиугольника!
Если сторона треугольника, с которого зачинается троичный путь равна √3
Сторона квадрата, начальника четверичного пути, равна √4
Можно предположить, что сторона пятиугольника будет равна √5 ...

Но я уже знаю, что это не так!

Быть может речь о десятиугольнике?
Проверю:

Отрезок φ = (√5-1) делит окружность радиусом 2 аршина на 10 частей.

По крайней мере лучше, чем невнятная мера √(2-φ).

В самом начале "Цветок жизни" сразу делит окружность вовсе не на 3 и 4, а на 6 и 8 частей.
Быть может древние работали именно с такими многоугольниками?
Нет, не нравится мне это. Дробить окружность на многоугольники можно сколь угодно долго и на каждом шаге будут появляться новые меры.

Должен быть простой и понятный приём, где многоугольники — лишь следствия, частные случаи, чьи размеры жёстко связаны с радиусом окружностей, в которую они вписаны!

В предыдущих частях я упоминал фигуру, известную как Vesica Piscics или Рыбий Пузырь, которая всегда образуется при пересечении окружностей.
Встречается в иконописи, орнаменталистике и храмовой архитектуре, мягко говоря, не редко.

Можно ли предположить, что именно этот "пузырь" является основным орудием творения?

Здесь пузыри порождают меру √3, но при этом они имеют разно расположение. В одном случае можно нарисовать равносторонний треугольник, вписанный в единичную окружность. В другом — описать окружность радиусом √3.

Пойду дальше.

Здесь получаем окружность радиусом √4 и делим её квадратом на 4 части. Можем на 8, 16, 32 и т.д. Двоить легко!

Вот мы и добрались до крепкого орешка — пятеричной тропки.
Особенность здесь в том, что пузыри пересекают середину, а не встречаются в ней, как в двух предыдущих случаях:

Уровень боковых лучей делит пополам сам пузырь на расстоянии φ и Ф от горизонтальной оси в аршинах. Можно сказать, что это синусы. Ну а косинусы относятся друг к другу в отношении Ф.

Середина чертежа делит пузырь в отношении φ², но здесь мера — двухаршинная малая сажень. Т.е надо разделить на 2, что бы получить золотой ряд от единицы: 0,7639320225/2=((√5-1)/2)²=0,381966011.
Т.е. мы имеем единицу и φ². Но где же φ? Получился какой-то провал.

Она прячется в десятиграннике:

Сторона десятигранника в малых саженях равна 1,2360679775/2=0,618033989=φ

Как и в предыдущих двух случаях мы наблюдаем единство многоугольников с удвоенной кратностью:
3 и 6,
4 и 8,
5 и 10.

Ну и в завершение.
Есть замечательная связь между рядом Фибоначчи и рядом Золотого сечения.
Она описывается формулой Бине:

Ряд Фибоначчи состоит из целых чисел.
Складывая или вычитая Ф и φ одинаковых степеней мы получаем диагональ сдвоенного квадрата. А деля на √5 — длинную сторону этого прямоугольника.
Красиво же...

Заключение счёта

Довольно трудно осознать значение и следствия сказанного.
Пожалуй, это можно назвать другой теорией чисел.

Как древо, стволом которого является общий для всех путей аршин, несущими ветвями - саженный строй, на котором произрастают веточки потоньше - дополнительные меры, присущие троичному и пятеричному пути.

Используя соответствующие случаю лучи и меры, действительно можно обойтись целыми положительными числами для выражения любых законов (формул), а значит построения любых правильных геометрических кривых и фигур.

Есть ещё простые числа — они в промежутках между. О них разговор особый.
В предыдущей работе я вывел правило их применения: Периметр квадрата со стороной 11 равен длине окружности радиусом 7.

Впрочем, тут ещё много особых разговоров...

Я предполагаю, что такой взгляд на счёт даст преимущества при работе в "поле квадратичных иррациональностей".
Однако в геометрии существует много задач, которые принципиально невозможно решить пользуясь лишь циркулем и линейкой.

Как ни удивительно - даже разделить окружность на 360 частей.
Хотя, казалось бы...

Геометрия статична. Она определяет законы, по которым происходит движение, но сама движением не является.
Разделив круг на несколько частей мы получили просто несколько частей.
Это ещё не счёт.
Счёт - это обороты.
Обороты - это перемещение в пространстве по времени.
Но что такое — Время?

Время

Время и пространство выражаются друг через друга понятием скорость. Например, в километрах в час, метрах в секунду. Или обратный случай - в днях пути.

Метр есть длина пути, проходимого светом в вакууме за интервал времени 1⁄299792458 секунды.

W:Метр

А что такое секунда?

Представляет собой интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, находящегося в покое при 0 К.

W:Секунда

Пери́од (от др.-греч. περίοδος — окружность, обход) — отрезок времени (или другой величины), определённый меткой начала отсчёта периода и меткой конца отсчёта периода.

W:Период

"Период излучения" - это волна, которая есть следствие вращения или колебания!
А вращение или дрожь (колебания, осцилляция) — это Время, которое создаётся оборотами!

Ведь если ничего не происходит — то и времени нет!

Движение определяется как скорость перемещения в пространстве, которое, в свою очередь измеряется временем.
Круг замкнулся.

Время — это последовательность неких движений, событий. Ток жизни - так об этом говорили раньше.
Следовательно время так же имеет некую мельчайшую частицу, подобно атому вещества или кванту силы:

В теории причинных множеств у пространства-времени есть “единицы” — пространственно-временные ‘атомы’. Таким образом теория накладывает ограничения на “близость” двух точек и двух событий. Они не могут быть ближе, чем на единицу пространства-времени.

“Течение времени [в теории причинных множеств] — это нечто физическое, его нельзя списать на иллюзию или процессы в нашем мозге, которые заставляют нас думать, что время идет; это течение времени само по себе и есть проявление физической теории, — объясняет Бенто. — В теории причинных множеств, множество будет увеличиваться на один ‘атом’ за раз и будет становиться больше и больше.”

Наука от Фансаенс, «Физики предположили, что у Вселенной не было начала»

Периоды излучения порождают волны, несущие Силу.

Мы не осознаём время, поскольку привыкли к его течению. Сиречь, к непрерывному вращению Земли!
Год - оборот вокруг Солнца.
День - оборот вокруг оси.
Дробим его на 24 части оборотами минутной стрелки часов.
И так далее.
Большая загадка, как мы чувствуем ход времени.
Профессиональные музыканты могут отбывать ритм с точностью атомных часов.
Но как они это делают?!
Видимо, мы связаны с мирозданием самой своей сутью.

А что же создаёт время?
Очевидно, некое постоянно повторяющееся действие. Например, вращение или колебание. Но чего?
Николай Александрович Магницкий в своей работе "Теория сжимаемого осциллирующего эфира" высказывает (и математически обосновывает) предположение, что это сфера.
Однако миф говорит нам о торе.

Пол

Полтора

Вот ты говоришь — МужЧина, ЖенЧина
Как две половины.

Однако Целое из Них есть Троица, иначе Тор.
Что есть половина Тора?
Пол Тора это ж так и есть —
Полтора, иначе половина Трёх!

Получается, что Мужчина и Женчина,
Их Пара, — каждый не по целому,
А по полтора?
Но Тор — всегда Один!

Это значит, что в каждом из Двоих
Есть то, и то — Бог и Диавол,
Истина и Идеал,
Мужчина и ЖенЧина,
Всё и Ничто,
Истинное и Мнимое,
Добро и Зло.
Всего — по мере. Четыре силы.
Так про — являет ся Господь.

***

Господь всем нужен.
Ибо с-Троить — значит быть с Троицей.
С Тора, с Трёх только и возможно созидание,
Иначе со-здание жизни.

Праведы

Здесь нет противоречия. В предельном случае тор неотличим от шара:

Так с первым шагом творения появляется сразу вся троица:
Первая волна образует расширяющуюся сферу: это несущая частота - C.
Длина волны - малая сажень (два аршина).
Скорость распространения - сажень за оборот.

Один оборот - это и есть мельчайшая частица времени (сиг?).
При этом обороты никак не различаются друг от друга - просто не существует каких-то признаков для их различения. Обороты повторяются раз за разом: Раз-Раз-Раз....
Мерять обороты можно лишь другими оборотами.

Но для начала нужно определить, выбрать Единицу.
Нужен тот самый Наблюдатель, с которым так отчаянно боролась, но без которого не смогла обойтись Наука.
Мир творится осознанием...

Игрец отличается от ученого, отличается принципиально, знаешь чем? Отношением со временем. Угу. Не ко времени, а со временем! — подчеркнул он. — Время — это лишь направление тока жизни. Были хорошие времена — жизнь течет в одну сторону, прибывает жизненная сила, и нам хорошо; худые времена настали — значит, направление тока жизни изменилось в противоположное, и нам плохо живется, потому что жизненная сила в мире убывает! Понимаешь?

— Это только способ говорить, — возразил я.

— Вот именно! А еще точнее, способ видеть мир, видеть жизнь, иначе говоря, способ сознавать. Но что важно, мир подчиняется нашему сознанию. Коммунизм тоже был всего лишь способом говорить, но Великой белой империи больше нет!
[…]
— А ты знаешь, какой практический вывод мы можем сделать из этого? Если от способа сознавать мир так много зависит, то мы можем поощрять, усиливать определенный образ видения мира и избегать другого. И если наша задача сделать жизнь хорошей, то мы должны служить этому, то есть быть жрецами жизни. Вот и получается, кто видит жизнь во всем, кто находит возможность даже сказку оживить — тот жрец жизни, а кто ищет способы, как уничтожить хоть что-то, хотя бы веру в сказку, тот жрец смерти! Вот чем занимается твоя наука, ну и соответственно, ученые…

А. Андреев, Игра и Игрецы

Время прямо связано с силой.
Сила нужна что бы запустить дрожь среды. Маятник или маховик в идеальных условиях (без трения) будет двигаться вечно. Но в самом начале должен быть толчок, который это движение запустит. Любое движение - суть накопленная, пойманная сила.
Значит тема моего следующего исследования определена...

Статья серии Cажени

<<<

>>>

При использовании материалов статьи активная ссылка на tart-aria.info с указанием автора Владимир Безуглов обязательна.